FUNÇÕES 09 - MÁXIMO E MÍNIMO DE UMA FUNÇÃO QUADRÁTICA

Demonstração dos pontos de Máximo e Mínimo de uma Função Quadrática

Definições:

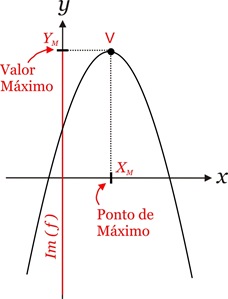
Valor de Máximo: Dizemos que o número Y_M ∈ Im (f) é o valor de máximo da função y = f(x) se, e somente se, Y_M ≥ y, ∀ y ∈ I_M (f). O número Y_M ∈ D(f) tal que Y_M = f(X_M) é chamado de ponto de máximo da função.

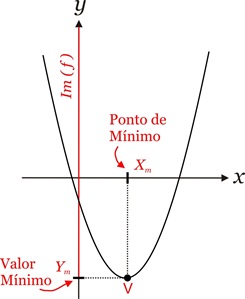
Valor de Mínimo: Dizemos que o número Y_m ∈ Im (f) é o valor de mínimo da funçãoy = f(x) se, e somente se, Y_M ≤ y, ∀ y ∈ I_m (f). O número Y_m ∈ D(f) tal que 

Y_m =f(X_m) é chamado de ponto de mínimo da função.

      

         

[Figura 1: Gráficos]

Teoremas:
1. Se a<0, a função quadrática y = ax²+bx+c admite o valor máximo Y_M = -Δ/4a
para    X_M = -b/2a.
2. Se a>0, a função quadrática y = ax²+bx+c admite o valor mínimo Y_m = -Δ/4a 
para    X_m = -b/2a.




Demonstração:

Para esta demonstração vamos primeiramente transformar a função quadráticay=ax²+bx+c em sua forma canônica.
Sedo f(x)=ax²+bx+c, podemos reescrevê-la na forma:

Então, colocamos a em evidência:

Se somarmos e subtrairmos um mesmo valor arbitrário de uma função, a mesma não sofrerá alteração em seu valor final. Utilizaremos, então, um valor conveniente igual ab²/4a²:



Vamos representar b² - 4ac por Δ, que é o discriminante do trinômio do 2º grau:

Temos então:

Se analisarmos a equação ( I ) mais minuciosamente, podemos concluir que, se a<0, o valor de y será tanto maior quanto menor for o valor da diferença:

E dessa diferença ( II ), podemos observar que:

• - Δ/4a² é constante, pois não depende da variável x, somente dos coeficientes a, b e c;
• , já que para quaisquer valores assumidos porx, a e b, (x+b/2a)² nunca será negativo, pois está elevado ao quadrado.

Podemos reescrever a diferença ( II ) como:







Vamos atribuir valores para x de modo a averiguar para quais valores assumidos por xleva a diferença ( II ) ao menor valor possível:


(– M + M)² – k =
0 – k =
– k
 
(1 – M + M)² – k =
1 – k



(2 – M + M)² – k =
4 – k


(– 3 – M + M)² – k =
9 – k
Vejam que para qualquer valor diferente de – M assumido por x, a diferença ( II ) aumenta. Portanto essa diferença assume o menor valor possível quando (x+b/2a)²=0, ou seja, quando x = – b/2a. Então:





Então, os valores do vértice da parábola serão:

e

Que são os valores para máximos e mínimos de uma equação de segundo grau.