CONCAVIDADE DE UMA FUNÇÃO

TEOREMA


Seja f uma função derivável pelo menos até segunda ordem num intervalo aberto I.
a) Se f''(x)>0 em I, então o gráfico de f terá concavidade para cima em I.
b) Se f''(x)<0 em I, então o gráfico de f terá concavidade para baixo em I.




Demonstração:


a) Seja a um ponto qualquer do intervalo I. Precisamos mostrar que, para todo 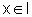, sendo 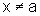, temos f(x)>T(x), onde T é a função cujo gráfico é a reta tangente ao gráfico de f no ponto (a,f(a)), isto é: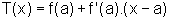


Consideremos a função g, tal que 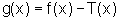, definida para todo .
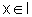Precisamos mostrar então que g(x)>0 para todo , .
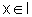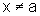Temos:


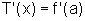
e, como,
,
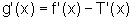então
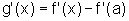, para .
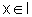Como, por hipótese, f''(x)>0 em I, segue que, pela primeira conseqüência do TVM, a função f ' é estritamente crescente em I.
Logo,
para x>a, 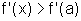 e, portanto ;
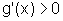para x<a, 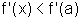 e, portanto .
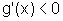Novamente, pela primeira conseqüência do TVM, aplicada à função g, temos que:
para x>a, g é estritamente crescente;
e para x<a, g é estritamente decrescente.
Como g(a)=0, temos g(x)>0 para todo x diferente de a.