RAIZ QUADRADA DE 2: O PRIMEIRO DOS IRRACIONAIS
Os pitagóricos são confrontados com os números irracionais.
Depois de durante milênios ter utilizado os números para contar, medir, calcular, o homem começou a especular sobre a natureza e propriedades dos próprios números. Desta curiosidade nasceu a Teoria dos Números, um dos ramos mais profundos da matemática. A Teoria dos Números nasceu cerca de 600 anos antes de Cristo quando Pitágoras e os seus discípulos começaram a estudar as propriedades dos números inteiros. Os pitagóricos rendiam verdadeiro culto místico ao conceito de número, considerando-o como essência das coisas. Acreditavam que tudo no universo estava relacionado com números inteiros ou razões de números inteiros (em linguagem atual, números racionais). Aliás, na antiguidade a designação número aplicava-se só aos inteiros maiores do que um. Esta crença foi profundamente abalada quando usaram o Teorema de Pitágoras para calcular a medida da diagonal de um quadrado unitário. Como eles apenas conheciam os números racionais (naturais e fracções de naturais) foi com grande surpresa e choque que descobriram que havia segmentos de recta cuja medida não pode ser expressa por um número racional. Essa descoberta é atribuída a um aluno de Pitágoras que tentava descobrir a medida da diagonal de um quadrado de lado 1.



Ao descobrirem que a diagonal de um quadrado de lado 1 não era uma razão entre dois inteiros (em linguagem actual, que a raíz quadrada de 2 é um número irracional) os Pitagóricos consideraram quebrada a harmonia do universo, já que não podiam aceitar a raíz quadrada de dois como um número, mas não podiam negar que esta raíz era a medida da diagonal de um quadrado unitário. Convencidos de que os deuses os castigariam caso divulgassem aquilo que lhes parecia uma imperfeição divina, tentaram ocultar a sua descoberta. Segundo reza a lenda, o primeiro membro da seita Pitagórica que divulgou esta descoberta morreu afogado num naufrágio sendo a sua alma açoitada pelas ondas para todo o sempre.
Assim, o número
terá sido o primeiro número irracional com que a humanidade se deparou.


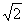
Nenhum comentário:
Postar um comentário