Zero: O número que tentaram proibir
Nos dias de hoje, todo estudante entende o significado do zero. Então porque será que, na história da humanidade, ele custou tanto a ser aceito?
Há evidências de que os primeiros sistemas de contagem tiveram início emaproximadamente 3000 a.C., no Egito,Mesopotâmia e Pérsia. (veja no mapa). No entanto, o surgimento do número zerose deu somente em torno de 300 a.C.
Não era preciso ter um número para expressar a falta de alguma coisa.
Não era preciso ter um número para expressar a falta de alguma coisa.
Duas concepções do Zero
Para entendermos bem a história do surgimento do zero, inicialmente temos que diferenciar os seus dois conceitos:
1) O zero como um símbolo, para representar o nada.
2) O zero como um número, usado nos cálculos.
É comum as pessoas pensarem que os dois são a mesma coisa, no entanto, a história nos mostra algo diferente.
O conceito do zero representando o nada, por ser mais fácil de perceber, também foi aquele que primeiramente se popularizou. Já para entender o surgimento do conceito de zero como número, é preciso antes compreender como funcionam os sistemas numéricos posicionais.
O conceito do zero representando o nada, por ser mais fácil de perceber, também foi aquele que primeiramente se popularizou. Já para entender o surgimento do conceito de zero como número, é preciso antes compreender como funcionam os sistemas numéricos posicionais.
O Sistema Numérico Posicional
O primeiro sistema posicional de números foi usado na Babilônia, a partir de 1800 a.C. Havia apenas dois símbolos. Um para o algarismos 1 e outro para o algarismo 10. Eles serviam para representar números até o 59(veja a tabela).
Os babilônios não agrupavam de 10 em 10 (base 10) como nós, mas sim, de 60 em 60. O sistema sexagesimal (base 60) teve sua origem especificamente na contagem do tempo. Até hoje, o sucesso desse sistema se reflete em nossas unidades de tempo e medidas de ângulos.
Para entender como surgiu a necessidade de acrescentar o zero aos numerais, vou utilizar dois números como exemplo: 61 e 3601.
No nosso sistema, de base 10, estes números poderiam ser representados assim:
Agora veja como estes mesmos números seriam representados nanumeração dos babilônios, de base 60:Para entender como surgiu a necessidade de acrescentar o zero aos numerais, vou utilizar dois números como exemplo: 61 e 3601.
No nosso sistema, de base 10, estes números poderiam ser representados assim:
Note que poderia haver confusão na interpretação. Para diferenciar um do outro, no caso da representação do número 3601, deixava-se um pequeno espaço entre os símbolos, que algumas vezes podia passar despercebido para o leitor.
A necessidade de diminuir esta ambiguidade tornou-se cada vez mais evidente, e isto deve ter se intensificado por volta de 300 a.C., quando então teria surgido pela primeira vez na história, um símbolo do número zero. Eles usaram duas pequenas flechas viradas para baixo. Veja:
Na Grécia clássica, a civilização certamente não estava preparada para encarar as complexidades do zero. O pensamento grego seguia a ideia de que os números expressavam formas geométricas. Então a que forma corresponderia algo que não existia de fato? A total ausência de algo - o vazio - era um conceito repudiado pela cosmologia dominante da época.
A filosofia oriental, enraizada nas idéias de ciclos eternos de criação e destruição, também não sentiria falta do zero. Ele encontrou apoio na Índia, através de matemáticos e astrônomos, como por exemplo, Brahmagupta, por vota de 628 d.C
Brahmagupta foi a primeira pessoa que começou a tratar os números como quantidades puramente abstratas, separadas de qualquer realidade fisica ou geométrica. Isso lhe permitiu considerar questões heterodoxas que os babilônios e gregos tinham ignorado ou dispensado, como o que acontece quando você subtrai de um número um número de maior tamanho. Em termos geométricos isto é um absurdo: Que área resta quando uma área maior é subtraída? Assim como os números se tornam entidades abstratas, por outro lado, um novo mundo de possibilidades se abre - O mundo dos números negativos
Brahmagupta foi a primeira pessoa que começou a tratar os números como quantidades puramente abstratas, separadas de qualquer realidade fisica ou geométrica. Isso lhe permitiu considerar questões heterodoxas que os babilônios e gregos tinham ignorado ou dispensado, como o que acontece quando você subtrai de um número um número de maior tamanho. Em termos geométricos isto é um absurdo: Que área resta quando uma área maior é subtraída? Assim como os números se tornam entidades abstratas, por outro lado, um novo mundo de possibilidades se abre - O mundo dos números negativos
Enquanto comerciantes e banqueiros rapidamente se convenceram da utilidade do sistema hindu-arábico, as autoridades eram menos apaixonadas. Em 1299, a cidade de Florença, Itália, proibiu o uso dos numerais hindu-arábicos, incluindo o zero. Eles consideraram que a capacidade de inflar enormemente o valor de um número simplesmente adicionando dígito ou dígitos no final - uma facilidade que não era disponível no então dominante sistema não-posicional dos algarismos romanos - poderia ser um convite aberto à fraude.
O número zero teve uma tarefa ainda mais difícil. Cismas, revoltas, reforma e contra-reforma na igreja significaram debates contínuos a respeito do valor das ideias de Aristóteles sobre o cosmos.
Só a revolução de Copérnico revelando que a Terra se move em torno do sol - começou, lentamente a agitar a matemática europeia na direção de livrar-se dos grilhões da cosmologia aristotélica, a partir doséculo 16.
O número zero teve uma tarefa ainda mais difícil. Cismas, revoltas, reforma e contra-reforma na igreja significaram debates contínuos a respeito do valor das ideias de Aristóteles sobre o cosmos.
Só a revolução de Copérnico revelando que a Terra se move em torno do sol - começou, lentamente a agitar a matemática europeia na direção de livrar-se dos grilhões da cosmologia aristotélica, a partir doséculo 16.
Por volta do século 17, a cena foi criada para o triunfo final do zero. É difícil apontar para um único evento marcante. Talvez tenha sido o advento do sistema de coordenadas inventado pelo filósofo e matemático francês René Descartes. Seusistema cartesiano unificava álgebra e geometria para dar a cada forma geométrica uma nova representação simbólica, com o zero como coração imóvel do sistema de coordenadas, em seu centro. O zero estava longe de ser irrelevante para a geometria, como os gregos haviam sugerido. Agora era essencial para ela.
Logo depois, a nova ferramenta de cálculo mostrou pela primeira vez como apreciar o nulo incorporado ao infinitamente pequeno para explicar como tudo no cosmos poderia mudar sua posição em tudo, tanto uma estrela como um planeta.
Logo depois, a nova ferramenta de cálculo mostrou pela primeira vez como apreciar o nulo incorporado ao infinitamente pequeno para explicar como tudo no cosmos poderia mudar sua posição em tudo, tanto uma estrela como um planeta.
Assim, uma melhor compreensão do zero tornou-se o fusível da revolução científica que se seguiu. Eventos subseqüentes confirmaram o quão essencial foi o zero para a matemática e tudo o que se edificou com ela.
 Olhando as diversas utilidades do zero hoje, é difícil imaginar como sua aceitação pôde ter causado tanta confusão e angústia.Definitivamente, um caso de muito barulho por nada.
Olhando as diversas utilidades do zero hoje, é difícil imaginar como sua aceitação pôde ter causado tanta confusão e angústia.Definitivamente, um caso de muito barulho por nada.
 Olhando as diversas utilidades do zero hoje, é difícil imaginar como sua aceitação pôde ter causado tanta confusão e angústia.Definitivamente, um caso de muito barulho por nada.
Olhando as diversas utilidades do zero hoje, é difícil imaginar como sua aceitação pôde ter causado tanta confusão e angústia.Definitivamente, um caso de muito barulho por nada.
fontes:
1 - http://www.bitlascado.com.br/post/A-Origem-do-Zero.aspx
2 - http://www.newscientist.com/article/mg21228390.500-nothingness-zero-the-number-they-tried-to-ban.html?DCMP=OTC-rss&nsref=magcontents
1 - http://www.bitlascado.com.br/post/A-Origem-do-Zero.aspx
2 - http://www.newscientist.com/article/mg21228390.500-nothingness-zero-the-number-they-tried-to-ban.html?DCMP=OTC-rss&nsref=magcontents
3 - http://raiosinfravermelhos.blogspot.com/2011/11/nosdias-de-hoje-todo-estudante-entende.html



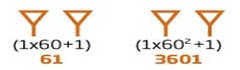



Interessante
ResponderExcluir