Breve Cronologia de PI
“Nós e todo o mundo guardamos PI usando letra por número”
A razão entre o perímetro de uma circunferência e seu diâmetro é dada por π (Pi), aproximadamente 3,141592. Foi exaustivamente estudado e historicamente temos que no Oriente antigo tomavam-se frequentemente 3 como uma aproximação de π. Para a quadratura do círculo egípcia encontrada no papiro de Rhind, temos π = (4/3)2 = 3,1604... . Porém, a primeira tentativa científica de calcular π parece ter sido se Arquimedes e será por esta realização que se inicia esta breve cronologia de π.
240 a.C.
Simplificando a questão, suponhamos um círculo de diâmetro unitário. Então o comprimento do círculo situa-se entre o perímetro de qualquer polígono regular inscrito e a de qualquer polígono regular circunscrito. Uma vez que é uma questão simples calcular os perímetros dos hexágonos regulares inscritos e circunscritos, facilmente se obtém limites para π. Mas há fórmulas que nos dizem, a partir de um par dado de polígonos regulares inscritos e circunscritos com o dobro de número de lados. Por aplicações sucessivas desse processo, podemos calcular os perímetros dos polígonos regulares inscritos e circunscritos de doze, vinte e quatro, quarenta e oito, noventa e seis lados, e dessa forma, obter limites cada vez mais próximos de π. Foi essencialmente isso que Arquimedes fez, chegando a conclusão de que π está entre 233/71 e 22/7 ou que, até a segunda casa decimal, π é dado por 3,14. Esse trabalho se encontra num tratado de Arquimedes, constituído de três preposições apenas e que se intitula A medida de um círculo. Esse tratado não chegou até nós em sua forma original e pode tratar-se apenas de um fragmento de uma discussão mais ampla. Considerando-se as limitações enormes do sistema de numeração de sua época, uma conclusão inevitável é que Arquimedes era um exímio calculista e, senão, o maior de sua época. Encontram-se no trabalho algumas aproximações racionais de raízes quadradas irracionais verdadeiramente notáveis.
Esse método utilizado por Arquimedes, baseado nos polígonos regulares inscritos e circunscritos é conhecido como método clássico de cálculo de π.
150
Depois de Arquimedes, a primeira aproximação notável de π foi dado por Cláudio Ptolomeu em sua famosa Syntaxis mathematica, mais popularmente conhecida comoAlmagesto, a maior obra de astronomia produzida na Grécia antiga. O valor de π nesta obra é, em notação sexagesimal, 38’30”, que é 377/120 ou 3,1416. Sem dúvida esse valor foi obtido a partir de uma tábua de cordas que há no tratado. A tábua fornece os comprimentos das cordas de um círculo correspondentes aos ângulos centrais de 0° a 180°, com incrementos de meio grau. Multiplicando-se o comprimento do diâmetro central de 1° por 360° e dividindo-se o resultado pelo comprimento do diâmetro do círculo, obtém-se o valor de π dado acima.
480
O mecânico chinês Tsu Ch'ung-chih deu a interessante aproximação racional 355/113 = 3,1415929... que é correta até a sexta casa decimal.
530
Um dos mais antigos matemáticos hindus, Äryabhata, deu 62832/20000 = 3,1416 como valor aproximado de π. Não se sabe exatamente como esse resultado foi obtido. Pode ser que tenha sido de fontes gregas mais antigas ou, talvez, do cálculo do perímetro de um polígono regular de 384 lados.
1150
O matemático hindu posterior, Bhäskara, deu várias aproximações de π. Deu 3927/1250 = 3,1416 com um valor acurado, 22/7 = 3,1428... como um valor impreciso e √10 como valor para trabalhos corriqueiros. O primeiro valor pode ter sido tomado de Äryabhata. É de origem incerta outro valor, 754/240 = 3,1416, dado por Bhäskara (trata-se do mesmo valor de Ptolomeu).
1429
Al-Kashi, assistente do astrônomo real de Samarcanda, Ulugh Beg, calculou π até a décima sexta casa decimal pelo método clássico.
1579
O eminente matemático francês François Viète encontrou π corretamente até a nona casa decimal pelo método clássico usando polígonos de 6(216) = 393.216 lados. Descobriu também o equivalente do interessante produto infinito:
1585
Adriaen Anthoniszoon redescobriu a antiga razão chinesa 355/113 = 3,14159292035... . Aparentemente foi um golpe de sorte, pois tudo que ele mostrou foi que 377/120 > π > 333/106. Ele então fez a média aritmética dos numeradores e dos denominadores para obter o valor "exato" de π. Há indícios de que Valentin Otho, um discípulo de Rhaeticus, um dos primeiros construtores de tábuas, pode ter introduzido essa razão para π no mundo ocidental numa data ligeiramente anterior, 1573.
1593
O holandês Adriaen van Roomen, masi conhecido como Adrianus Romanus, determinou π corretamente até a décima quinta casa decimal pelo método clássico, usando polígonos de 230 lados.
1610
O holandês Ludolph can Ceulen calculou π até a trigésima quinta casa decimal pelo método clássico, usando polígonos de 262 lados. Ceulen gastou grande parte de sua vida nessa tarefa e seu feito foi considerado tão extraordinário que sua viúva fez gravar o número em seu túmulo (hoje perdido) no adro da igreja de São Pedro em Leyden. Até hoje o número π é às vezes chamado de "número ludophiano".
1621
O físico holandês Willebrord Snell, mais conhecido por sua descoberta da lei da refração, descobriu um aperfeiçoamento trigonométrico do método clássico de calcular π tal que, de cada par de limites para π dado pelo método clássico, ele era capaz de obter limites consideravelmente mais próximos. Com seu método conseguiu obter as trinta e cinco casas decimais de vanCeulen apenas com polígonos de 230. Com esses polígonos, o método clássico fornece apenas quinze casas. Para polígonos de noventa e seis lados, o método clássico fornece duas casas decimais, ao passo que o aperfeiçoamento de Snell fornece sete casas decimais. Em 1654 o matemático e físico holandês Chistiaan Huygens forneceu uma demonstração correta do refinamento de Snell.
1630
Usando o refinamento de Snell, Grienberger calculou π até a trigésima nona casa decimal. Essa foi a última tentativa importante de calcular π pelo método clássico.
1650
O matemático inglês John Wallis obteve a curiosa expressão:
Lord Brouncker, o primeiro presidente da Royal Society, converteu o resultado de Wallis na fração contínua:
Nenhuma dessas expressões, porém, serviu para um cálculo longo de π.
1671
O matemático escocês James Gregory obteve a série infinita:
Passou despercebido a Gregory que, para x = 1, a série torna-se:
Essa série, que converge muito lentamente, era conhecida de Leibniz em 1674. Gregory tentava provar que é impossível uma solução euclidiana do problema da quadratura do círculo.
1699
Abraham Sharp encontrou acertadamente as primeiras setenta e uma casas decimais de π usando a série de Gregory para:
1706
John Machin obteve cem casas decimais usando a série de Gregory juntamente com a relação:
1719
O matemático francês De Lagny obteve corretamente 112 casas decimais usando a série de Gregory para:
1737
O símbolo π fora usado fora usando anteriormente pelos matemáticos ingleses Willian Oughtred, Isaac Barrow e David Gregory para designar a circunferência de um círculo. O primeiro a usar esse símbolo para a razão entre a circunferência e o diâmetro foi o escritor inglês Willian Jones, numa publicação de 1706. Porém, o símbolo só encontrou aceitação geral depois que Euler o adotou em 1737.
1754
O francês Jean Étienne Montucla, um dos primeiros historiadores da matemática, escreveu uma história do problema da quadratura.
1755
A Academia de Ciências da França declinou examinar qualquer solução mais do problema da quadratura.
1767
Johann Heinrich Lambert provou que π é irracional.
1777
O conde de Buffon concebeu seu famoso problema da agulha pelo qual pode-se aproximar π por métodos probabilísticos. Suponhamos que se tracem num plano horizontal um número grande de retas paralelas equidistantes entre si. Sendo d a distância entre duas retas vizinhas quaisquer, Buffon mostrou que a probabilidade de que uma agulha de comprimento L < d, lançada ao acaso sobre o plano, caia cortando uma das retas é dada por:
Realizando-se efetivamente esse experimento um número grande de vezes e anotando-se os casos positivos, obtém-se um valor empírico de π que podemos usar na fórmula acima para calcular uma aproximação de π. O melhor resultado por este caminho foi conseguido pelo italiano Lazzerini em 1901. Com 3408 lançamentos da agulha ele obteve π corretamente até a sexta casa decimal! Seu resultado é superior ao de outros experimentos às vezes visto com suspeição; Há outros métodos probabilísticos para calcular π. Assim é que, em 1904, R. Chartes relatou uma aplicação do conhecido fato de que se dois inteiros positivos são escritos ao acaso, a probabilidade de que eles sejam primos entre si é de 6/π2.
1794
Adrien-Marie Legendre mostrou que π2 é irracional.
1841
O inglês Willian Rutherfird calculou π com 208 casas (com 152 corretas, como se mostrou depois) usando a série de Gregory juntamente com a relação:
1844
O calculista relâmpago Zacharias Dase encontrou π corretamente até a ducentésima casa decimal usando a série de Gregory juntamente com a relação:
Dase, que nasceu em Hamburgo em 1824, morreu prematuramente aos trinta e sete anos de idade. Talvez tenha sido ele o mais extraordinário calculista mental de todos os tempos. Dentre suas façanhas, figura o cálculo mental do produto de dois números de vinte algarismos em seis minutos, de dois números de quarenta algarismos em quarenta minutos e de dois números de cem algarismos em oito horas e quarenta minutos. Calculou também a raiz quadrada de um número de cem dígitos em cinquenta e dois minutos. Dase fez um uso mais valioso de seus poderes quando construiu uma tábua de logaritmos naturais de sete casas e uma tábua de fatores de todos os números entre 7.000.000 e 10.000.000.
1853
Rutherford retornou ao problema e obteve corretamente 400 casas decimais.
1853
O inglês Willian Shanks, usando a fórmula de Machin, calculou π com 707 casas decimais. Por um longo tempo foi feito mais fabuloso em termos de computação.
1882
Um número se diz algébrico se é raiz de algum polinômio não-nulo de coeficientes racionais; caso contrário, se diz transcendente. F. Lindermann provou que π é transcendente. Esse fato garante que o problema da quadratura não pode ser resolvido com os instrumentos euclidianos.
1906
Dentre as curiosidades ligadas a π há várias mnemônicas que foram concebidas para memorizar esse número até um número grande de casas decimais. Os seguintes versos em inglês, de A.C.Orr, apareceram no Literary Digest. Basta substituir cada palavra pelo número de letras que a compõe para obter π corretamente até a trigésima casa decimal:
Now I, even I, would celebrate In rhymes unapt, the great Immrtal Syracusan, rivaled nevermore, Who in his wondrous lore, Passed on before, Left men his guidance, How to circles mensurate.
Uns anos mais tarde, em 1914, apareceu a seguinte mnemônica semelhante noScientific American Supplement: "See, I have a rhyme assisting my feeble brain, its tasks ofttimes resisting." Eis outras duas mnemônicas: "How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics" e"May I have a large container os coffe?"
1948
Em 1946 o inglês D.F.Ferguson descobriu erros, começando na 528ª casa, no valor encontrado por Shanks para π e em 1947 deu um valor correto com 710 casas. No mesmo mês o americano J.W.Wrench Jr. publicou o valor de π com 808 casas, mas Ferguson encontrou em erro na 723ª casa. Em janeiro de 1948 Ferguson e Wrench publicaram juntamente um valor correto e testado de π com 808 casas. Wrench usou a fórmula de Machin, ao passo que Ferguson usou a fórmula:
1949
O ENIAC, computador eletrônico do Amy Ballistic Research Laboratories de Aberdeen, Maryland, calculou π com 2037 casas decimais.
1959
François Gennuys, em Paris, calculou π com 16.167 casas decimais, usando um IBM704.
1961
Wrenchi e Daniel Schanks de Washington, DC., calculou π com 1.000.265 casas decimais usando um IBM7090.
1965
O ENIAC, agora obsoleto, foi desmontado e transportado para o Smithsonian Institution como peça de museu.
1966
Em 22 de fevereiro, M. Jean Guilloud e seus colegas de trabalho na Comissão de Energia Atômico de Paris obtiveram uma aproximação de π que alcançava 250.000 casas decimais, num computador STRETCH.
1967
Exatamente um ano depois, os mesmos pesquisadores usando um CD6600, encontraram uma aproximação de π com 500.000 casas.
1973
Guilloud e seus colegas encontraram uma aproximação de π com 1.000.000 de casas num CDC7600.
1981
Os dois matemáticos japoneses Kazunori Miyoshi e Kazuhika Nakayama, da Universidade de Tsukuba, calcularam π com 2.000.038 algarismos em 137,30 horas, num computador FACOM-M200. Eles usaram a fórmula:
e testaram seu resultado na fórmula de Machin.
1986
Em janeiro deste ano, D. H. Bailey da NASA, Ames Research Califórnia, fez funcionar uma supercomputador Cray-2 por 28 horas para obter π com 29.360.000 dígitos. Seu código baseava-se num algoritmo de J. M e P. D. Borwein da Universidade Dalhousie Bailey, testou seu código num algoritmo mais lento, também desenvolvido pelos Borwein e verificou a precisão de seu trabalho. Pouco depois, Yasumasa Kanada, da Universidade de Tóquio, usando um supercomputador NEC SX-2 e o algoritmo dos Borwein, calculou π com 13.721.700 dígitos.
No cálculo de π com um número grande de casas decimais há outras questões: Ante de 1767, quando provou-se que π é irracional, uma das razões era verificar se os dígitos de π começavam a se repetir e, se fosse esse o caso, obtê-lo como um número racional exato, talvez com um denominador grande. Mas, recentemente, a motivação é conseguir informações estatísticas referentes à “normalidade” de π.
Um número real se diz simplesmente normal se em sua expansão decimal todos os dez primeiros algarismos ocorrem com igual frequência; e se diz normal se todos os blocos de algarismos de um mesmo comprimento ocorrem com igual frequência. Não se sabe se π (ou mesmo √2) é normal ou mesmo simplesmente normal.
Os cálculos de π, começando pelo ENIAC em 1949, foram realizados para fornecer informações estatísticas sobre a questão.
Em relação à possível normalidade de π é interessante que a sequência 314159 dos seis primeiros algarismos de π, aparecem seis vezes nos primeiros dez milhões de dígitos da expansão de π e a sequência 0123456789 não aparece nunca.
Analogamente, a sequência 271828 dos seis primeiros dígitos de e, base do logaritmo natural, ocorre oito vezes nos primeiros dez milhões de algarismos da expansão decimal de e.Referências
[1] Introdução à História da Matemática; Eves, Howard; ed. Unicamp

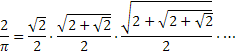
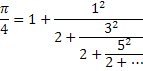
Nenhum comentário:
Postar um comentário