Use a transformação ![]() e
e ![]() para calcular a integral
para calcular a integral
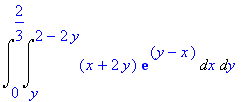
primeiro escrevendo-a como uma integral sobre uma região G no plano 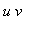 .
.
RESOLUÇÃO:
Dos extremos de integração percebe-se que a região de integração é limitada pelas retas ![]() e
e ![]() com y no intervalo
com y no intervalo ![]() . Essa região está ilustrada na figura abaixo.
. Essa região está ilustrada na figura abaixo.
Por outro lado, com a transformação dada, tem-se
Logo, as retas ![]() e
e ![]() no plano Oxy correspondem às retas
no plano Oxy correspondem às retas ![]() = 0 e
= 0 e ![]() = 2 no plano Ouv. Além disso, como
= 2 no plano Ouv. Além disso, como ![]() , a reta
, a reta ![]() no plano Oxy corresponde à reta
no plano Oxy corresponde à reta ![]() no plano Ouv. A figura abaixo ilustra a região G no plano Ouv correspondente à região no plano Oxy
no plano Ouv. A figura abaixo ilustra a região G no plano Ouv correspondente à região no plano Oxy
Para o cálculo da integral, é necessário calcular o jacobiano da transformação, que é o determinante da matriz
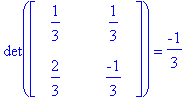
Finalmente, usando a fórmula de mudança de variáveis, segue-se que
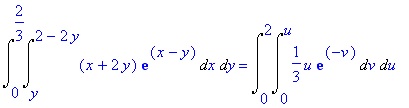
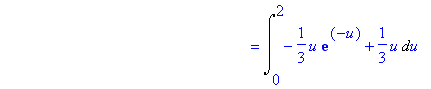
Essa é uma integral dupla!
ResponderExcluirO método da transformação é muito eficaz e facilmente compreende-se muito bom mesmo!
ResponderExcluirQuanto aos planos oxy correspondentes as rectas no plano cartesiano também estão muito bem explicado.
ResponderExcluir