(a) A maneira usual de calcular a integral imprópria ![]()
é primeiro calcular o seu quadrado
Calcule essa integral usando coordenadas polares e resolva a equação resultante para encontrar I.
(b) Calcule
RESOLUÇÃO:
(a) Em coordenadas polares, o primeiro quadrante corresponde ao domínio em que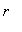 
está no intervalo ( 
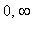) e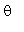 
está no intervalo ( ![]()
). Daí segue-se que, em coordenadas polares,
está no intervalo ( ) e está no intervalo (
onde a integral na variável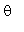 
é imediata e a integral na variável 
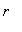é fácil de ser calculada! De fato, com a substituição ![]()
tem-se que
é imediata e a integral na variável é fácil de ser calculada! De fato, com a substituição
Daí segue-se que
e portanto ![]()
(b) Do item anterior é claro agora que
Como curiosidade, a figura abaixo ilustra o gráfico da função ![]()
no intervalo 
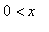(na cor vermelha), bem como o gráfico da função ![]()
no primeiro quadrante. O valor de 
corresponde ao volume abaixo do gráfico de 
, enquanto que 
corresponde à área abaixo do gráfico de 
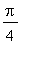(na cor vermelha), bem como o gráfico da função corresponde ao volume abaixo do gráfico de 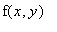, enquanto que 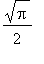corresponde à área abaixo do gráfico de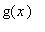 
Nenhum comentário:
Postar um comentário