Em dois tipos de botijões (56 litros e 72 litros) qual o número mínimo de botijões devemos ter para comportar 328 litros?
Pelo enunciado temos que resolver a equação diofantina (solução indeterminada inteira):
56x + 72y = 328
Seja o cálculo do mdc(72,56)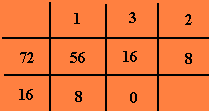
72 = 1.56 + 16 (1)
56 = 3. 16 + 8 (2)
16 = 2.8
De (1), temos que:
16 = 1.72 - 1.56 (3)
Substituindo (3) em (2), temos que:
56 = 3.(1.72 - 1.56) + 8, ou seja 8 = 4.56 - 3.72
Paremos aqui e tenhamos em mente da teoria dos números que:
"Sejam a, b e c inteiros e d= mdc(a,b). A equação diofantina aX + bY = c tem solução se e somente se d é divisor de c"
e também
"Sejam a, b, c inteiros tais que d=mdc(a,b) divide c.Escrevendo d na forma d = ra + sb, com r e s inteiros, temos que: x0 = r.c/d e y0 = s.c/d como solução particular de aX+bY=c e x=r.c/d + (b/d)t e y = s.c/d - (a/d)t como solução genérica de aX+bY=c"
Voltando onde paramos, temos que:
r = 4 e s = -3
Como solução particular teríamos: x0 = 4.328/8 = 164 e y0 = -3.328/8 = -123
Vemos que não nos serve pois o valor de y é negativo
Verifiquemos, então, a solução genérica:
x =164 + 72/8 t = 200 + 9t e y = -123 - 56/8 t = -150 -7t (4)
Como precisamos que x > 0 e y > 0, então
164 + 9t > 0 e -123 - 7t > 0
ou seja: t > -18,1 e t < - 17,5 (5)
A solução inteira que satisfaz (5) é t = 18
Substituindo esse valor em (4), temos que:
x = 2 e y = 3, que respondem ao enunciado do problema.

Nenhum comentário:
Postar um comentário