Mude a integral cartesiana
para uma integral polar equivalente. Então calcule a integral polar.
RESOLUÇÃO:
Para x no intervalo [-1, 1], as curvas ![]() e
e ![]() descrevem os semi-círculos inferior e superior do círculo de raio 1. Logo, a região de integração é o disco de raio 1. A figura abaixo ilustra esse disco juntamente com o gráfico da função
descrevem os semi-círculos inferior e superior do círculo de raio 1. Logo, a região de integração é o disco de raio 1. A figura abaixo ilustra esse disco juntamente com o gráfico da função ![]() .
.
Em coordenadas polares ![]() e
e ![]() , o disco pode ser descrito como o conjunto dos pontos (
, o disco pode ser descrito como o conjunto dos pontos ( 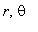 ) para os quais
) para os quais 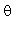 está no intervalo (
está no intervalo ( ![]() ) e
) e 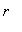 está no intervalo (
está no intervalo ( ![]() ). Essa variação está ilustrada na figura abaixo.
). Essa variação está ilustrada na figura abaixo.
Após essas considerações, e lenbrando que, em coordenadas polares, ![]() , segue-se que
, segue-se que
Isto transforma a integral cartesiana em uma integral polar equivalente. Para o cálculo da integral polar, basta usar a substituição ![]() . Então
. Então ![]() , e portanto
, e portanto
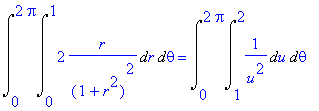
Nenhum comentário:
Postar um comentário