Esse blog é de caráter pessoal e destina-se aos alunos e companheiros interessados em Matemática.
Sendo a internet uma vasta rede de informações que se perde em quantidade de conteúdo, o que pretendemos é juntar todas essas informações em um local que meus alunos possam ter acesso de forma mais simples. Logo para construção desse blog o que estamos fazendo é garimpando na rede tudo que consideramos relevante e postando em um único lugar.

sexta-feira, 16 de março de 2012

DIVISÃO EUCLIDIANA E O TEOREMA FUNDAMENTAL DA ARITMÉTICA

Divisão euclidiana e o teorema fundamental da aritmética

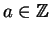
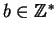
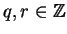
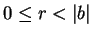
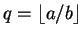
A divisão euclidiana, ou divisão com resto, é uma das quatro operações que toda criança aprende na escola. Sua formulação precisa é: dados $a \in {\mathbb{Z} }$, $b \in {\mathbb{Z} }^\ast$existem $q, r \in {\mathbb{Z} }$ com $0 \le r < \vert b\vert$ e a= bq + r. Tais q e r estão unicamente determinados e são chamados o quociente e resto da divisão de a por b. 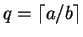Se b > 0 podemos definir $q = \lfloor a/b \rfloor$ e se b < 0, $q = \lceil a/b \rceil$; em qualquer caso, r = a -bq. 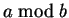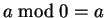O resto r é às vezes denotado por $a \bmod b$; definimos $a \bmod 0 = a$. 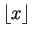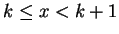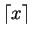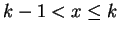Lembramos que $\lfloor x \rfloor$ denota o único inteiro k tal que $k \le x < k + 1$ e $\lceil x \rceil$ o único inteiro k tal que$k - 1 < x \le k$.
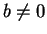
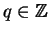
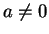
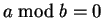
Dados dois inteiros a e b (em geral com $b \ne 0$) dizemos que b divide a, ou que a é um múltiplo de b, e escrevemos b | a, se existir $q \in {\mathbb{Z} }$ com a = qb. Se $a \ne 0$, também dizemos que b é um divisorde a. Assim, b | a se e somente se $a \bmod b = 0$.
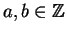
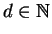
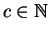
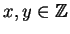
Proposição 1.1: Dados $a, b \in {\mathbb{Z} }$ existe um único $d \in {\mathbb{N} }$ tal que d|a, d|b e, para todo $c \in {\mathbb{N} }$, se c|a e c|b então c|d. Além disso existem $x, y \in {\mathbb{Z} }$ com d = ax + by.
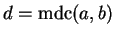
Esse natural d é chamado o máximo divisor comum, ou mdc, entre a e b. Escrevemos $d = \operatorname{mdc}(a, b)$ ou (se não houver possibilidade de confusão) d = (a,b).
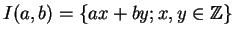
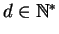
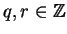
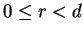
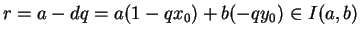
Dem: O caso a = b = 0 é trivial (temos d = 0). Nos outros casos, seja $I(a,b) = \{ax + by; x, y \in {\mathbb{Z} }\}$ e seja d = a x0 + b y0 o menor elemento positivo de I(a,b). Como $d \in {\mathbb{N} }^\ast$, existem$q, r \in {\mathbb{Z} }$ com a = dq + r e $0 \le r < d$. Temos $r = a - dq = a (1 - q x_0) + b (- q y_0) \in I(a,b)$; como r < d e d é o menor elemento positivo de I(a,b), r = 0 e d | a. Analogamente, d | b. Suponha agora que c|a e c|b; temos c | a x + b y para quaisquer valores de x e ydonde, em particular, c|d.          $\blacksquare$
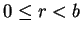
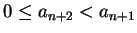
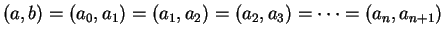
O algoritmo de Euclides para calcular o mdc baseia-se nas seguintes observações simples. Se a = bq + r, $0 \le r < b$, temos (com a notação da demonstração acima) I(a,b) = I(b,r), donde (a,b) = (b,r). Definindo a0 = a, a1 = b e an = an+1 qn+2 + an+2, $0 \le a_{n+2} < a_{n+1}$(ou seja, an+2 é o resto da divisão de an por an+1) temos $(a,b) = (a_0,a_1) = (a_1,a_2) = (a_2,a_3) = \cdots = (a_n,a_{n+1})$para qualquer valor de n. Seja N o menor natural para o qual aN+1 = 0: temos (a,b) = (aN,0) = aN.
Lema 1.2: Se (a, b) = 1 e a|bc então a|c.
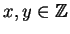
Dem: Como (a, b) = 1, existem $x, y \in {\mathbb{Z} }$ com ax + by = 1, logo a | c = acx + bcy.          $\blacksquare$
Quando (a,b) = 1 dizemos que a e b são primos entre si. Um natural p > 1 é chamado primo se os únicos divisores positivos de p são 1 e p. Um natural n > 1 é chamado composto se admite outros divisores além de 1 e n.
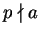
Claramente, se p é primo e $p \nmid a$ temos (p,a) = 1. Usando o lema anterior e indução temos o seguinte resultado:
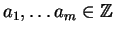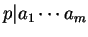Corolário 1.3: Sejam p um número primo e sejam $a_1, \ldots a_m \in {\mathbb{Z} }$. Se $p\vert a_1 \cdots a_m$ então p|ai para algum i, 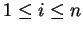$1 \le i \le n$.
Estamos agora prontos para enunciar e provar o teorema que diz que todo inteiro admite fatoração única como produto de primos.
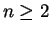
Teorema 1.4: (Teorema fundamental da aritmética) Seja $n \ge 2$ um número natural. Podemos escrever n de uma única forma como um produto

\begin{displaymath}n = p_1 \cdots p_m\end{displaymath}


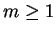
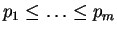
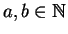
onde $m \ge 1$ é um natural e $p_1 \le \ldots \le p_m$ são primos.Dem: Mostramos a existencia da fatoração por indução. Se n é primo não há o que provar (escrevemos m = 1, p1 = n). Se n é composto podemos escrever n = ab, $a, b \in {\mathbb{N} }$, 1 < a < n, 1 < b < n. Por hipótese de indução, a e b se decompõem como produto de primos. Juntando as fatorações de a e b(e reordenando os fatores) obtemos uma fatoração de n.
Vamos agora mostrar a unicidade, também por indução. Suponha que

\begin{displaymath}n = p_1 \cdots p_m = q_1 \cdots q_{m'},\end{displaymath}


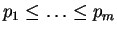
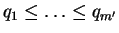
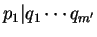
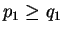
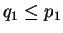
com $p_1 \le \ldots \le p_m$, $q_1 \le \ldots \le q_{m'}$. Como $p_1 \vert q_1 \cdots q_{m'}$ temos p1 | qi para algum valor de i, donde, como qi é primo, p1 = qi e $p_1 \ge q_1$. Analogamente temos $q_1 \le p_1$, donde p1 = q1. Mas por hipótese de indução

\begin{displaymath}n/{p_1} = p_2 \cdots p_m = q_2 \cdots q_{m'}\end{displaymath}


admite uma única fatoração, donde m = m' e pi = qi para todo i.          $\blacksquare$Outra forma de escrever a fatoração é

\begin{displaymath}n = p_1^{e_1} \cdots p_m^{e_m},\end{displaymath}


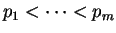
com $p_1 < \cdots < p_m$, ei > 0. Ainda outra formulação é escrever

\begin{displaymath}n = 2^{e_2} 3^{e_3} 5^{e_5} \cdots p^{e_p} \cdots\end{displaymath}


onde o produto é tomado sobre todos os primos mas apenas um número finito de expoentes é maior do que zero.Segue deste teorema o outro algoritmo comum para calcular o mdc de dois números: fatoramos os dois números e tomamos os fatores comuns com os menores expoentes. Este algoritmo é bem menos eficiente do que o de Euclides para inteiros grandes (que em geral não sabemos fatorar) mas é instrutivo saber que os dois algoritmos dão o mesmo resultado.
Corolário 1.5: Se (a,n) = (b,n) = 1 então (ab,n) = 1.
Dem: Evidente a partir do algoritmo descrito acima.          $\blacksquare$
Teorema 1.6: (Euclides) Existem infinitos números primos.
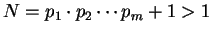
Dem: Suponha por absurdo que p1, p2,..., pm fossem todos os primos. O número $N = p_1 \cdot p_2 \cdots p_m + 1 > 1$não seria divisível por nenhum primo, o que contradiz o teorema fundamental da aritmética.          $\blacksquare$
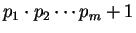
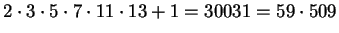
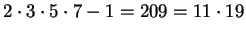
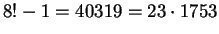
Observe que não provamos que $p_1 \cdot p_2 \cdots p_m + 1$é primo para algum conjunto finito de primos (por exemplo, os m primeiros primos). Aliás, $2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 + 1 = 30031 = 59 \cdot 509$,$2 \cdot 3 \cdot 5 \cdot 7 - 1 = 209 = 11 \cdot 19$, 4! + 1 = 25 = 52 e $8! - 1 = 40319 = 23 \cdot 1753$ não são primos. Não existe nenhuma fórmula simples conhecida que gere sempre números primos.

Fonte: http://www.mat.puc-rio.br/~nicolau/papers/mersenne/node4.html

Postado por às
Marcadores:

Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)