Calcule a área de um círculo de raio r.
O Cálculo Integral nos permite calcular precisamente a área de um círculo de raio dado.
Em primeiro lugar, vamos estabelecer um sistema de eixos cartesianos, a fim de poder descrever a circunferência como o gráfico de duas funções:
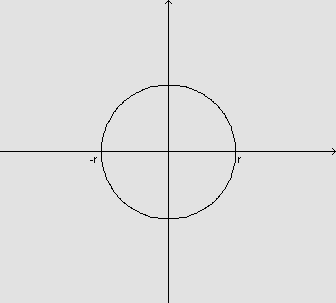
Uma vez que
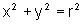 é a equação da circunferência de centro na origem e raio r, podemos escrever:
é a equação da circunferência de centro na origem e raio r, podemos escrever: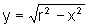 ou
ou 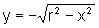 .
.
A área da região delimitada pelo eixo horizontal e pelo gráfico de 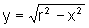 , ou seja a área de um dos semi-círculos, é dada por:
, ou seja a área de um dos semi-círculos, é dada por:
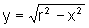 , ou seja a área de um dos semi-círculos, é dada por:
, ou seja a área de um dos semi-círculos, é dada por: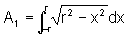 .
.
Uma vez que a função integrando é uma função par, podemos apenas calcular a área de um quarto do círculo, ou seja:
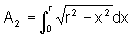 .
.
A fim de calcular a família de primitivas, isto é, 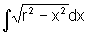 , fazemos a substituição:
, fazemos a substituição:
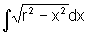 , fazemos a substituição:
, fazemos a substituição: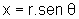 , para
, para 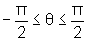
temos:
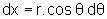 .
.
Logo
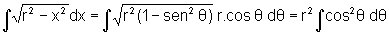
pois se 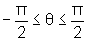 ,
, 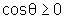 e, além disso,
e, além disso, 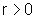 .
.
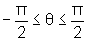 ,
, 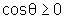 e, além disso,
e, além disso, 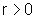 .
.
temos:
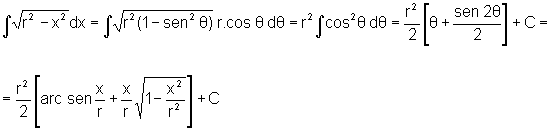
Logo,
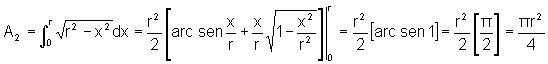 .
.
Como 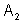 é a área de um quarto do círculo, a área do círculo inteiro é
é a área de um quarto do círculo, a área do círculo inteiro é 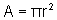 .
.
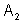 é a área de um quarto do círculo, a área do círculo inteiro é
é a área de um quarto do círculo, a área do círculo inteiro é 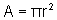 .
.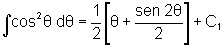
Nenhum comentário:
Postar um comentário