Demonstração de Funções Trigonométricas do Arco Duplo
É possível deduzir fórmulas para calcular as funções trigonométricas de 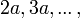 utilizando as fórmulas obtidas para a soma de arcos e fazendo
utilizando as fórmulas obtidas para a soma de arcos e fazendo 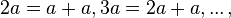 conforme será mostrado adiante.
conforme será mostrado adiante.


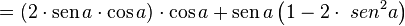
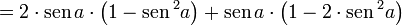

calcule



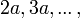 utilizando as fórmulas obtidas para a soma de arcos e fazendo
utilizando as fórmulas obtidas para a soma de arcos e fazendo 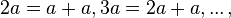 conforme será mostrado adiante.
conforme será mostrado adiante.
Cosseno
Usando a fórmula do cosseno da soma, temos:

Logo, utilizando a identidade trigonométrica, podemos obter duas fórmulas finais:
ou



Utilizando a Identidade trigonométrica e trabalhando algebricamente, temos:
Expressões para  são obtidas por processos semelhantes.
são obtidas por processos semelhantes.
 são obtidas por processos semelhantes.
são obtidas por processos semelhantes.Seno
Ultilizando a fórmula do seno da soma:
Então, temos:
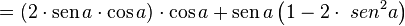
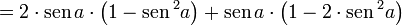
Logo:
Expressões para  são obtidas por processos semelhantes.
são obtidas por processos semelhantes.
 são obtidas por processos semelhantes.
são obtidas por processos semelhantes.Tangente
A partir da fórmula da tangente da soma:

Logo:
Ao subtituimos a fórmula anterior para 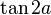 e simplificarmos, obtemos como fórmula final:
e simplificarmos, obtemos como fórmula final:
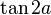 e simplificarmos, obtemos como fórmula final:
e simplificarmos, obtemos como fórmula final:
Expressões para  são obtidas por processos semelhantes.
são obtidas por processos semelhantes.
 são obtidas por processos semelhantes.
são obtidas por processos semelhantes.Exemplo
Se
 e
e 
calcule 
Resolução
Precisamos encontrar  para aplicarmos a fórmula. Para tanto, utilizaremos a identidade
para aplicarmos a fórmula. Para tanto, utilizaremos a identidade 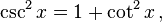 que relaciona as funções cotangente e cossecante. A partir da cossecante obtida, podemos encontrar o valor do seno, uma vez que
que relaciona as funções cotangente e cossecante. A partir da cossecante obtida, podemos encontrar o valor do seno, uma vez que 
 para aplicarmos a fórmula. Para tanto, utilizaremos a identidade
para aplicarmos a fórmula. Para tanto, utilizaremos a identidade 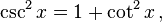 que relaciona as funções cotangente e cossecante. A partir da cossecante obtida, podemos encontrar o valor do seno, uma vez que
que relaciona as funções cotangente e cossecante. A partir da cossecante obtida, podemos encontrar o valor do seno, uma vez que 
Como  o valor da cossecante é positivo.
o valor da cossecante é positivo.
 o valor da cossecante é positivo.
o valor da cossecante é positivo.
De onde vem

Podemos finalmente calcular:

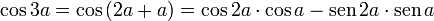







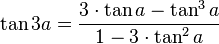
Nenhum comentário:
Postar um comentário