MATEMÁTICA É ASSIM, TAMBÉM !: O anel das classes de congruência

quarta-feira, 13 de junho de 2012

O anel das classes de congruência

Sempre que se tem uma relação de equivalência $\sim$ sobre um conjunto $X$ é possível definir uma partição $P$ de tal conjunto. Uma coleção $P$ de subconjuntos de $X$ é chamada de partição de $X$ se todo elemento de $X$ pertence a exatamente um elemento de $P$ . Os elementos de $P$ são disjuntos dois a dois, e sua união é o próprio conjunto $X$ .
Para definir uma partição de $\mathbb{Z}$ , usando a congruência módulo $m$ , primeiramente define-se para cada inteiro $a$ a classe de equivalência de $a$ , segundo $\sim$ , como:

$[a]_m = \{ x \in \mathbb{Z}; x \equiv a \!\!\!\!\pmod{m}\}$

Quando o inteiro $m$ estiver subentendido, será utilizado apenas $[a]$ para denotar $[a]_m$ .
Nesses termos, o quociente de $\mathbb{Z}$ pela relação $\equiv \!\!\!\!\pmod{m}$ é a partição dada por:

$\mathbb{Z}/_{\equiv \!\!\!\!\pmod{m}} = \{[a]_m; a \in \mathbb{Z}\}$

Por simplicidade, denota-se $\mathbb{Z}/_{\equiv \!\!\!\!\pmod{m}}$ simplesmente como 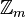$\mathbb{Z}_m$ .
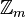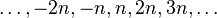Uma das formas de visualizar essa partição de $\mathbb{Z}$ é imaginar que sobre um barbante foram marcados todos os números inteiros, separando os números adjacentes sempre por uma mesma distância. Depois disso, para obter uma representação de $\mathbb{Z}_m$ , enrola-se o barbante em torno de uma circunferência (infinitas vezes!), de modo que o zero ocupe a mesma posição que os inteiros $\ldots, -2n, -n, n, 2n, 3n, \ldots$ . Você pode então pensar nos elementos de $\mathbb{Z}_n$ como sendo os n pontos sobre a circunferência que se formou. Veja uma ilustração:

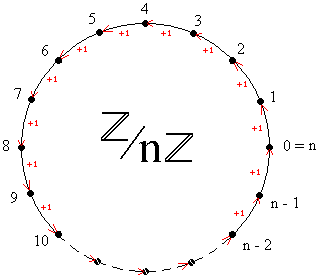
Representação dos inteiros módulo n sobre uma circunferência.

Deste modo, cada ponto da circunferência representa uma das classes de equivalência módulo $n$ , ou seja, o conjunto dos números inteiros que ficaram sobrepostos naquele ponto da circunferência.
Mas o que há de interessante em particionar o conjunto dos números inteiros?
A grande utilidade de separar os números inteiros em várias classes de congruência é consequência da compatibilidade da congruência com as operações de adição e multiplicação: Sabendo-se que elas são compatíveis, é possível definir em cada 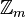$\mathbb{Z}_m$ novas operações de adição e multiplicação. O procedimento é o seguinte:
Fixado um inteiro $m$ , e dadas as classes $[a], [b]$ , define-se:

$[a] + [b] = [a + b]$

$[a] \times [b] = [a \times b]$ (ou simplesmente $[a] [b] = [a b]$ )

Em outras palavras, a soma (produto) das classes de congruência dos inteiros $a, b$ é a classe de congruência de sua soma (produto).
É importante notar onde é utilizada a compatibilidade da congruência com as operações de $\mathbb{Z}$ : Dadas duas classes de equivalência $A=[a]=[a']$ e $B=[b]=[b']$ , tanto faz obter $[A]+[B]$ como sendo $[a+b],[a'+b],[a+b']$ ou $[a'+b']$ . Todas essas classes são idênticas!
Mais do que isso, ao definir essas operações, $(\mathbb{Z}_m, +, \times)$ torna-se um anel com unidade, ou seja, são válidas as seguintes propriedades:
Além disso, tem-se um homomorfismo de anéis entre $\mathbb{Z} = \{ 0, \pm 1, \pm 2, \pm 3, \ldots \}$ e $\mathbb{Z}_m = \{ m\mathbb{Z} + 0, m\mathbb{Z} + 1,\ldots , m\mathbb{Z} + (m-1) \}$ :

$\rho: \mathbb{Z} \rightarrow \mathbb{Z}_m$

$\rho(x) = [x] = [x \!\!\!\!\pmod{m}]$

MATEMÁTICA É ASSIM, TAMBÉM !

quarta-feira, 13 de junho de 2012

O anel das classes de congruência

Nenhum comentário:

Postar um comentário