Definição
- Definição
O inteiro  é dito congruente ao inteiro
é dito congruente ao inteiro 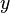 módulo
módulo  , quando
, quando  . Neste caso, escreve-se
. Neste caso, escreve-se 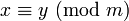 .
.
 é dito congruente ao inteiro
é dito congruente ao inteiro 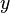 módulo
módulo  , quando
, quando  . Neste caso, escreve-se
. Neste caso, escreve-se 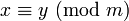 .
.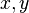 :
: e
e  módulo
módulo  , a soma de dois quadrados nunca é congruente a
, a soma de dois quadrados nunca é congruente a  módulo
módulo  .
. |
0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 2 |
 .
.- Nota


 )
que não são relevantes durante grande parte dos cálculos envolvendo
divisibilidade. Atente para a semelhança (visual) entre as seguintes
expressões:
)
que não são relevantes durante grande parte dos cálculos envolvendo
divisibilidade. Atente para a semelhança (visual) entre as seguintes
expressões:



Nenhum comentário:
Postar um comentário