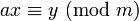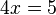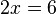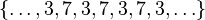Esse blog é de caráter pessoal e destina-se aos alunos e companheiros interessados em Matemática.
Sendo a internet uma vasta rede de informações que se perde em quantidade de conteúdo, o que pretendemos é juntar todas essas informações em um local que meus alunos possam ter acesso de forma mais simples. Logo para construção desse blog o que estamos fazendo é garimpando na rede tudo que consideramos relevante e postando em um único lugar.
sexta-feira, 29 de junho de 2012
domingo, 17 de junho de 2012
LINKS PARA OS PAPMEM DE TODOS OS ANOS
- Janeiro de 2001
- Janeiro de 2002
- Julho de 2002
- Janeiro de 2003
- Julho de 2003
- Janeiro de 2004
- Julho de 2004
- Janeiro de 2005
- Julho de 2005
- Janeiro de 2006
- Julho de 2006
- Janeiro de 2007
- Julho de 2007
- Janeiro de 2008
- Julho de 2008
- Janeiro de 2009
- Julho de 2009
- Janeiro de 2010
- Julho de 2010
- Janeiro de 2011
- Julho de 2011
- Janeiro de 2012
PAPMEM: Julho de 2005
- Geometria Analítica do Plano - Prof. Elon (IMPA)
- Combinatória I - Prof. Morgado (IMPA)
- Volumes I - Prof. Wagner (IMPA)
- Geometria Analítica no Espaço - Prof. Elon (IMPA)
- Aplicações de Geometria Analítica - Prof. Paulo Cezar (IMPA)
- Combinatória II - Prof. Morgado (IMPA)
- Volumes II - Prof. Wagner (IMPA)
- Probabilidades - Prof. Paulo Cezar (IMPA)
- Discussão - 1a parte (IMPA)
- Discussão - 2a parte (IMPA)
PAPMEM: Janeiro de 2005
- Função Exponencial - Prof. Elon (*) (IMPA)
- Funções Trigonométricas -Prof. Paulo Cezar (Funções Trigonométricas) (IMPA)
- Aplicações Trigonométricas - Prof. Wagner (IMPA)
- Logarímos - Prof. Elon (IMPA)
- Geometria Espacial de Posição - Prof. Paulo Cezar (Geometria Espacial de Posição) (IMPA)
- Progressções - Prof. Morgado (IMPA)
- Poliedros - Prof. Wagner (IMPA)
- Matem&aactive;tica Financeira - Prof. Morgado (IMPA)
- Discussão I - Todos (IMPA)
- Discussão II - Todos (IMPA)
- Programa de Som utilizado na aula de Funções Trigonométricas
PAPMEM: Julho de 2004
- Conjuntos e Números Naturais - Prof. Elon (IMPA)
- Indução - Prof. Morgado (IMPA)
- Números Cardinais - Prof. Elon (IMPA)
- Números Reais - Prof. Paulo Cezar (IMPA)
- Função Afim - Prof. Wagner (IMPA)
- Função Quadrática - 1a parte - Prof. Paulo Cezar (IMPA)
- Função Quadrática - 2a parte - Prof. Wagner (IMPA)
- Funções Polinomiais - Prof. Morgado (IMPA)
- Discussão - 1a parte (IMPA)
- Discussão - 2a parte (IMPA)
PAPMEM: Janeiro de 2004
- Equação do Segundo Grau I - Prof. Elon (IMPA)
- Triàngulo Retàngulo I - Prof. Wagner (IMPA)
- Problemas de Contagem - Prof. Morgado (IMPA)
- Trigonometria - Prof. Paulo Cezar (IMPA)
- Triàngulo Retàngulo II - Prof. Wagner (IMPA)
- Equação do Segundo Grau II - Prof. Elon (IMPA)
- Problemas de Segundo Grau - Prof. Morgado (IMPA)
- Probabilidade - Prof. Paulo Cezar (IMPA)
- Discussão I - Todos (IMPA)
- Discussão II - Todos (IMPA)
PAPMEM: Julho de 2003
- Proporcionalidade - 1a parte (IMPA)
- Equações do Primeiro Grau - 1a parte (IMPA)
- Áreas - 1a parte (IMPA)
- Estatística - 1a parte (IMPA)
- Proporcionalidade - 2a parte (IMPA)
- Equações do Primeiro Grau - 2a parte (IMPA)
- Áreas - 2a parte (IMPA)
- Estatística - 2a parte (IMPA)
- Discussão - 1a parte (IMPA)
- Discussão - 2a parte (IMPA)
- Vídeo "The Story of PI"
- Vídeo "Similarity"
sábado, 16 de junho de 2012
PAPMEM: Janeiro de 2003
- Funções Quadráticas (IMPA)
- Funções Trigonométricas (IMPA)
- Recorrèncias (IMPA)
- Funções Exponenciais e Logarítmicas I (IMPA)
- Aplicações de Trigonometria (IMPA)
- Aplicações de Funções Quadráticas (IMPA)
- Polinômios (IMPA)
- Funções Exponenciais e Logarítmicas II (IMPA)
- Discussão - 1a parte (IMPA)
- Discussão - 2a parte (IMPA)
- Comentários Jacob Palis - Diretor do Impa (IMPA)
quarta-feira, 13 de junho de 2012
PAPMEM: Janeiro de 2001
Link para o vídeo do PAPMEM - janeiro de 2001
- 22-01-01 - 09:15 - 10:30 - Professor Elon - Proporcionalidade e Funções Afins download
- 22-01-01 - 10:45 - 12:00 - Professor Wagner - Aplicações da Trigonometria download
- 23-01-01 - 09:15 - 10:30 - Professor Elon - Funções Quadráticas I download
- 23-01-01 - 10:45 - 12:00 - Professor Morgado - Noções de Matemática Financeira download
- 24-01-01 - 09:15 - 10:30 - Professor Paulo Cezar - Funções Exponenciais I download
- 24-01-01 - 10:45 - 12:00 - Professor Wagner - Introdução ao Cálculo de Volumes download
- 25-01-01 - 09:15 - 10:30 - Professor Elon - Funções Quadráticas II download
- 25-01-01 - 10:45 - 12:00 - Professor Morgado - Combinatória I download
- 26-01-01 - 09:15 - 10:30 - Professor Paulo Cezar - Funções Exponenciais II download
- 26-01-01 - 10:45 - 12:00 - Professor Morgado - Combinatória II download
Equações lineares - Congruências
Equações lineares
Uma questão muito natural é investigar em que casos há alguma solução para equações lineares do tipoExemplo de equação linear com apenas uma solução
Considere em a seguinte equação:
a seguinte equação: , é possível determinar
, é possível determinar  tais que
tais que e
e  . Outra possibilidade é
. Outra possibilidade é 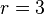 e
e  . Neste caso, nota-se que:
. Neste caso, nota-se que: em
em  , ou seja, que neste anel o inverso multiplicativo de
, ou seja, que neste anel o inverso multiplicativo de  é ele mesmo. Sabendo disso, é possível resolver
é ele mesmo. Sabendo disso, é possível resolver : Multiplicando-se ambos os membros pelo inverso de
: Multiplicando-se ambos os membros pelo inverso de  , segue:
, segue: para a equação dada. Observe ainda que o número
para a equação dada. Observe ainda que o número 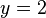 não teve qualquer influência no número de soluções para o problema. Isso pode ser percebido considerando para cada
não teve qualquer influência no número de soluções para o problema. Isso pode ser percebido considerando para cada  o resultado de sua multiplicação por
o resultado de sua multiplicação por 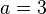 :
:-
0 1 2 3 4 5 6 7 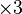
0 3 6 1 4 7 2 5
 e que, portanto, o único elemento que é levado em
e que, portanto, o único elemento que é levado em  ao ser multiplicado por
ao ser multiplicado por  é o
é o  . Essa unicidade permaneceria se o
. Essa unicidade permaneceria se o  fosse trocado por qualquer outro elemento.
fosse trocado por qualquer outro elemento.Exemplo de equação linear sem solução
Considere a seguinte equação em :
: :
: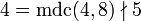 .
.Exemplo de equação linear com duas soluções
Como um último exemplo antes de conhecer o teorema que dá uma resposta definitiva sobre o número de soluções de uma equação linear em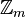 , considere em
, considere em  a equação:
a equação: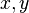 tais que:
tais que: , devemos considerar os números acima módulo
, devemos considerar os números acima módulo  :
: equações do tipo
equações do tipo 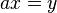 que possuam uma ou duas soluções, e mesmo equações que não adimitem solução. Essa é uma notavel diferença entre corpos (como
que possuam uma ou duas soluções, e mesmo equações que não adimitem solução. Essa é uma notavel diferença entre corpos (como  ,
,  e
e 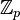 ) e anéis. Por exemplo, em
) e anéis. Por exemplo, em  ou
ou  você deve estar habituado a resolver
você deve estar habituado a resolver 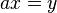 , simplesmente dividindo os dois membros por
, simplesmente dividindo os dois membros por  (e talvez descrevendo esse procedimento como "passar o
(e talvez descrevendo esse procedimento como "passar o  para o lado direito, dividindo..."). No entanto, é tempo de notar que isso só é possível quando
para o lado direito, dividindo..."). No entanto, é tempo de notar que isso só é possível quando  possui inverso. Em
possui inverso. Em  ,
todo número não nulo possui inverso. Mas isso não é verdade em todo
anel! Por essa razão torna-se necessário tomar algum cuidado ao resolver
equações nos aneis
,
todo número não nulo possui inverso. Mas isso não é verdade em todo
anel! Por essa razão torna-se necessário tomar algum cuidado ao resolver
equações nos aneis 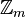 . Fique atento!
. Fique atento!
Assinar:
Comentários (Atom)