A raiz quadrada de 2 não é um número racional:
Demonstração
Aristóteles (384-322 a.C.), como exemplo de uma demonstração por redução ao absurdo, demonstrou que a raiz quadrada de 2 não é um número racional, isto é, não se pode escrever como uma fracção de dois números inteiros. Por absurdo, suponha-se que existem dois números naturais p e q, primos entre si, tais que
(isto é, suponhamos a fracção
 escrita na forma irredutível) e
escrita na forma irredutível) e  .
.
e, consequentemente, p também é par (porque se fosse ímpar seria
seria ímpar). Se p é um número par, existe um natural k tal que





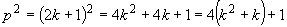



Nenhum comentário:
Postar um comentário