domingo, 8 de janeiro de 2012

FUNÇÕES 10 - CONVEXIDADE


Convexidade


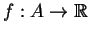
Uma função $f:A\rightarrow \Bbb{R}$ é dita convexa em um intervalo $\left[ a,b\right] \subseteq A$ se para todo $0<s<1$,

\begin{displaymath} f\left( a+s\left( b-a\right) \right) \leq f\left( a\right) +s\left( f\left( b\right) -f\left( a\right) \right) \text{.} \end{displaymath}


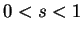
Se a desigualdade for estrita, dizemos que 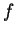$f$ é estritamente convexa. A função é dita convexa no seu domínio 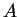$A$ se for convexa em todo intervalo $\left[ a,b\right] \in A$. De modo análogo, define-se uma função côncava, apenas substituindo a desigualdade acima pela desigualdade 
\begin{displaymath} f\left( a+s\left( b-a\right) \right) \geq f\left( a\right) +s\left( f\left( b\right) -f\left( a\right) \right) \text{.} \end{displaymath}
às

Nenhum comentário:

Postar um comentário