INTEGRAIS DUPLAS - EXERCÍCIO RESOLVIDO

EXERCÍCIO:

Esboce a região de integração, inverta a ordem de integração e calcule a integral

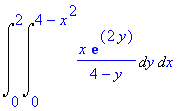
RESOLUÇÃO:

Segundo os extremos de integração, para cada x no intervalo [0, 2], y varia no intervalo  . Essa variação está indicada em vermelho na figura abaixo, em que foi usada a notação  . A região de integração está indicada em azul claro.

Para inverter a ordem de integração, observe que a mesma região pode ser descrita da seguinte forma: para cada y no intervalo [0, 4], x varia de 0 até 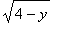 . Essa variação está indicada em azul na figura acima, onde foi usada a notação  . Com essa descrição obtém-se que

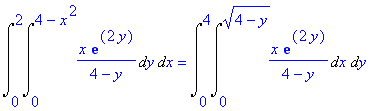
A vantagem dessa inversão é que, agora, as integrais podem ser calculadas de forma simples. De fato, a primeira integral a ser feita é

A segunda integral é igualmente fácil, sendo igual a

o que concluí a resolução do exercício.