Encontre o volume do sólido que é limitado superiormente pelo cilíndro
RESOLUÇÃO:
A figura abaixo ilustra os gráficos das funções ![]() (em vermelho) e
(em vermelho) e ![]() (em azul). Do gráfico é claro que, se D é a região limitada por essas curvas, então D é uma região do tipo Rx que pode ser descrita como D = {(x, y);
(em azul). Do gráfico é claro que, se D é a região limitada por essas curvas, então D é uma região do tipo Rx que pode ser descrita como D = {(x, y); 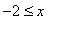
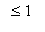 e
e 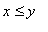
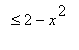 }.
}.
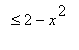 }.
}.
Esboçando o domínio acima juntamente como o cilíndro ![]() , obtém-se o gráfico abaixo, que é uma ilustração do sólido.
, obtém-se o gráfico abaixo, que é uma ilustração do sólido.
Da ilustração acima é claro que o volume procurado corresponde à integral da função ![]() sobre o domínio D. Calculando, obtém-se que o volume é dado por
sobre o domínio D. Calculando, obtém-se que o volume é dado por
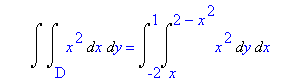
Nenhum comentário:
Postar um comentário