(1+r)n 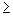 1+r.n, para todo r > 0.
1+r.n, para todo r > 0.
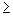 1+r.n, para todo r > 0.
1+r.n, para todo r > 0.
(1+r)n 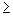 1+r.n.
1+r.n.
Vamos escrever P(1): (1+r)=1+r.1. Portanto, P(1) vale.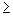 1+r.n.
1+r.n.Suponhamos agora que vale P(k), ou seja, (1+r)k
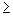 1+r.k
1+r.kVerifiquemos que, se vale P(k), então vale P(k+1), isto é, (1+r)k+1
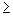 1+r.(k+1)
1+r.(k+1)Temos: (1+r)k+1= (1+r)k.(1+r)
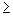 (1+r.k).(1+r) = 1+r.k+r+r2.k
(1+r.k).(1+r) = 1+r.k+r+r2.k 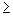 1+ r.(k + 1),
1+ r.(k + 1),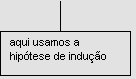
Logo, P(n) vale para todo n
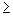 1.
1.Observemos que, para n=0, a propriedade também vale, pois
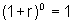 e 1+r.0=1. Portanto, P(n) vale para todo
e 1+r.0=1. Portanto, P(n) vale para todo 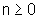 .
.
Nenhum comentário:
Postar um comentário