Definição de Função
Se a cada valor de uma variável
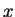
corresponde a um único valor de uma outra variável
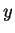
, então
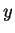
é uma
função (de uma variável) de
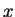
e podemos expressá-la simbolicamente como
Dado um conjunto de números reais 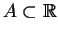 e uma função
e uma função 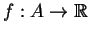 , dizemos que
, dizemos que 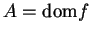 é o domínio de
é o domínio de 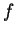 ,
, 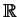 é o contra-domínio e o conjunto
é o contra-domínio e o conjunto 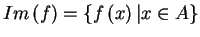 é a imagem de
é a imagem de 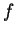 .
.
Nenhum comentário:
Postar um comentário