Exercício 2
Encontre o volume da região no primeiro octante limitada pelos planos coordenados, pelo plano
Solução
A região está ilustrada na figura abaixo, em que o cilindro ![]()
está em azul e o plano ![]()
em ocre.
Indique por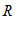 
a região da qual se quer calcular o volume. Da figura percebe-se que a base 
de 
é a região triangular descrita da seguinte maneira: para cada 
fixo no intervalo [0, 4], 
varia no intervalo ![]()
.
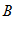a região da qual se quer calcular o volume. Da figura percebe-se que a base de 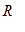é a região triangular descrita da seguinte maneira: para cada 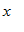fixo no intervalo [0, 4], 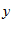varia no intervalo
Isolando o valor de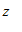 
da expressão do cilíndro, obtém-se que ![]()
. Daí segue-se que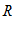 
pode ser descrita como: para cada (x, y) fixo na base B, z varia no intervalo![]()
. Usando essa descrição, segue-se que o volume V de 
é dado pela integral tripla
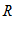da expressão do cilíndro, obtém-se que pode ser descrita como: para cada (x, y) fixo na base B, z varia no intervalo é dado pela integral tripla
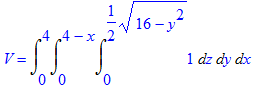
Calculando essa integral iteradamente, obtém-se que o volume da região é dado por
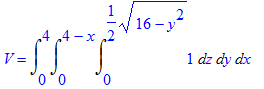
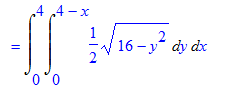
Nenhum comentário:
Postar um comentário