Use a transformação ![]() e
e ![]() para calcular a integral
para calcular a integral
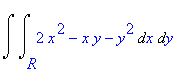
para a região R no primeiro quadrante limitada pelas retas ![]() ,
, ![]() ,
, ![]() e
e ![]() .
.
RESOLUÇÃO:
A região R está ilustrada na figura abaixo.
Observe que, com a transformação dada, tem-se ![]() e
e ![]() . Logo, as retas
. Logo, as retas ![]() e
e ![]() no plano Oxy correspondem às retas horizontais
no plano Oxy correspondem às retas horizontais ![]() e
e ![]() no plano Ouv. Analogamente, as retas
no plano Ouv. Analogamente, as retas ![]() e
e ![]() no plano Oxy correspondem às retas verticais
no plano Oxy correspondem às retas verticais ![]() e
e ![]() no plano Ouv. A figura abaixo ilustra a região no plano Ouv correspondente à região R
no plano Ouv. A figura abaixo ilustra a região no plano Ouv correspondente à região R
Para o cálculo da integral, primeiro é necessário calcular o jacobiano da transformação, que é o determinante da matriz
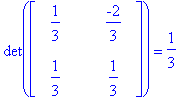
Segundo, substituindo ![]() e
e ![]() no integrando, obtém-se
no integrando, obtém-se
Logo, usando a fórmula de mudança de variáveis, segue-se que
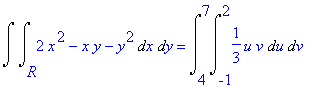
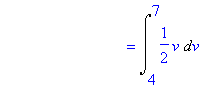
Nenhum comentário:
Postar um comentário